一、深层次把握高中数学公式学习和数学素养的关系

高中数学公式学习难度较大，学习是否牢固、扎实，直接影响到不同类型数学知识的学习。尤其是在高考压力下，需要掌握更具针对性的学习方法。在掌握数学公式的同时，还要注重学生数学素养的培养，便于学生逐步内化数学知识，完善知识结构。此种方式有助于筑牢后续数学知识学习的基础，还可以促进学生身心健康成长。数学是一门理科学科，各种公式之间联系密切，如函数与数列的关系。三角函数与函数奇偶性的关系。仅仅依靠死记硬背难以实现对数学知识的高效理解和记忆。这就需要将高中数学公式整合在一起，创新逻辑性较强的思维模式，鼓励学生在分析问题和讨论问题时掌握关联数学公式。在此基础上延伸拓展，加深学生的认识逻辑，有效促进学生核心素养发展。

二、把握公式约束条件避免乱用

高中数学教学中，很多数学公式的应用是有着明确约束条件的。在对数运算中，数的加减法运算需要设定真数大于0的前提条件。直线方程中学生喜欢用点斜式来计算直线方程式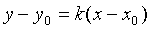，但很多情况下可能有漏解问题的出现，因为这个方程式应用有着明显的约束条件，斜率k不存在的直线是不含在内的。数列中可以得到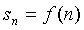，在计算求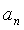之类的题型中，运算解题可以直接套用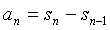进行计算，但却忽视了这个公式应用是需要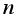不小于2的，n=1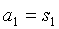，。这就导致很多学生在解题时出现了失误，增加解题难度。因此，教师要保持严谨性，在讲解公式的运用时明确约束条件，尽可能减少丢分项，提升解题准确率。此外，使用数学公式来解题，不要过于死板，而是要活学活用，多角度去分析和理解题目，灵活运用公式去解题，从而显著提升学生的知识运用能力。教师也要注意发挥自身的引导作用，不要为了追求教学进度或是完成教学任务，盲目要求学生按照既定思路解题。帮助学生掌握数学公式，拓宽解答面，找到更适合自己的解题方法才是重中之重，这对于学生的数学核心素养发展有着深远的意义。

三、在实际情境中发展直观想象

在高中数学教学中，直观想象是学生通过空间形式解决问题的重要数学素养，简单来说就是通过几何直观与空间想象来对事物的形态和变化进行感知，是发现问题、提出问题、分析问题以及解决问题的重要手段，将其应用于公式教学中，有利于培养学生的论证思维和推理思维。例如，在人教版高中数学教材《三角函数》中，教师可以利用学生比较熟悉的摩天轮来展开相关教学活动，展示相关图形，让学生发散思维，分组讨论和思考摩天轮的点与地面距离应当如何进行表示。学生利用图形的特点建立起直角坐标系，同时对摩天轮上的点到地面的距离利用三角函数的定义来列举公式，即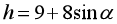。这种从实际出发来创设情境的教学，不仅能够有效地激发出学生的学习热情，同时也能够帮助学生用数学公式来表达问题，从而使学生能够更为深入地了解到三角函数的知识点，并且使其懂得利用知识点来刻画相关周期现象。教师可以进一步地提出问题进行引导，比如:“在这个公式中，如果角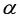等于150°，那么应当如何计算点P到地面的距离?”学生通过对图形进行观察，能够发现角150°与角30°的终边关于y轴对称，也就是说150°与角30°的终边与单位圆的交点纵坐标相等，因此两个角的正弦是相等的。有了这个基础，学生便能够很轻松地算出点P到地面的距离。教师在对学生进行引导时，应当侧重于图形的观察，让学生能够察觉到单位圆交点与互补角的终边是位于同一水平线，地面与两点之间的距离相等，最终得出结论，即其正弦值相等，这种教学方法能够牢牢抓住诱导公式这一教学本质，通过教学模型来得出结论能够使得学生更为直观地了解公式，进而促使学生更为灵活地应用三角函数的诱导公式。

四、合作学习，提升能力

　1.请学生进行小组讨论，总结出两角差的余弦公式的特点有哪些。设计意图：教师通过对学生的课堂指导，让学生与学生之间进行讨论，引导学生们一起总结和探索公式的规律特点。这样既加深了学生们对于数学公式的记忆，也为之后的课程学习做了铺垫。使学生对于后续所学习的知识点不再陌生恐惧，而是积极地参与其中。

2.学生根据公式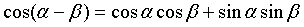来思考，并证明出两角和的余弦公式。设计意图：培养学生类比推理的能力，让学生学会使用化归数学思想。教师通过课堂教学，也可观察出学生对于问题的逻辑推理能力强弱，为之后的教学工作提供了参考，指明了方向。同时，也让学生对之前学习的两角差的余弦公式进行了巩固，使学生拥有了对数学知识大胆猜想的能力。

结束语

总而言之，在高中数学公式教学中，教师将核心素养培养作为教育目标，并融合到课堂教学中，有着深刻的意义。这种新的教学方式，更加符合新课程改革的要求，提高学生的综合素质。同时，也提高了教师的教学质量，提高了学生的学习效率，使学生的学习不再像以往那样沉闷，让高中数学的课堂更加鲜活生动。

参考文献

[1]王丹峰.基于核心素养的高中数学公式教学探析——以“三角函数的诱导公式”教学为例[J].延边教育学院学报,2019,33(03):197-198+203.

[2]聂颖.基于高中数学核心素养的公式教学研析——以“两角和与差的余弦”为例[J].数学之友,2018(05):27-29+34.