比较数与式的大小一直是高考的热点。高考对本部分内容的要求，主要是指数式、对数式的互化，以及构造函数比较大小。前些年通常考查利用幂函数、指数函数与对数函数的单调性比较大小，近几年考查趋势转移到构造复杂的函数，利用导数研究所构造函数的单调性，再通过赋值比较大小。要求学生具有一定的数学运算素养、以及分析问题解决问题的能力，主要考查数学运算与逻辑推理的核心素养。

2022年新高考数学1卷第7题，充分体现了这一理念，是考查“构造函数比较大小”的一道好题，下面我们一起来分析这道题目。

本题考查比较大小问题，难度较大，关键难点是将各个值中的共同的量用变量替换，构造函数，通过移项构造函数的方法构造新函数，利用导数研究相应函数的单调性，进而比较大小，这样的问题，凭借近似估计计算往往是无法解决的．

解法二：

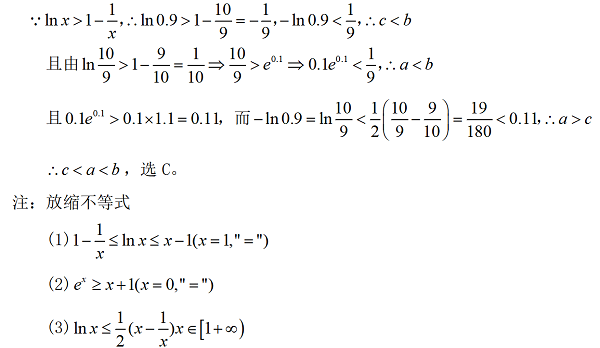
该思路主要是根据题干数与式的特点进行赋值，得出不等关系式，其实也是再利用得出的不等关系作为条件，利用不等式性质进行推理论证。对于出现频率较高的放缩不等式，笔者认为要熟记活用。

解法三：

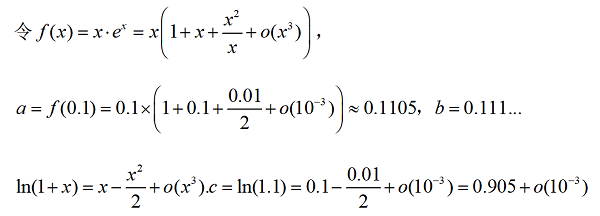
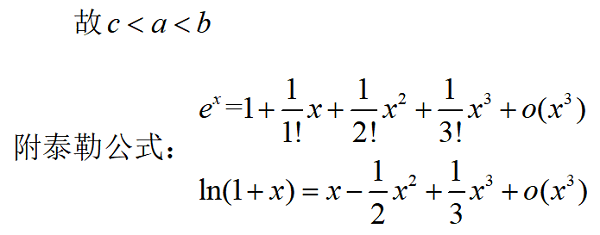
该思路解法的背景源于，全日制普通高中教科书（必修）《数学第一册》（2009年版）复习参考题5拓广探索第26题：英国数学家泰勒发现了如下公式：，，根据泰勒公式构造函数，在高中阶段也理解成二项式定理的应用。泰勒公式（二项式定理）在这里能将一些复杂的函数变成我们熟悉的多项式函数，能起到化繁为简的功能，在近似计算、不等式证明等方面发挥着重要的作用。  

通过一道高考真题对构造函数比较大小进行研析，笔者认为从近年来课改试题的特点来看，此类题目加大了思维量，减少了运算量，主要培养学生探索能力和思维能力，尽管运算量不大，但思维灵活，有较大难度，不仅考查指数函数、对数函数，还考查了利用导数求单调性，不等式性质等基础知识，同时考查了推理论证能力，分析问题和解决问题的能力，培养逻辑推理、数学建模、数学运算等数学核心素养。