一、模型的历史与价值

1. 在中等教育物理教材中的地位和作用。

各版高中物理教材都无一例外地用了这一模型，人教版现行教材是以习题形式出现，教科版教材是以活动形式出现，个人认为教科版的活动形式最能体现“过程与方法”，最能引导学生观察问题、分析问题，还能通过实验探究问题，因此选用教材编排，一方面使高考复习真正回归教材，体现教材的基础价值，更体现教材引领学生分析问题、解决问题能力提高。另一方面让学生通过此例真正领悟教材的魅力，在高考复习中真正把教材作为本。

2. 在历届高考试题中的呈现

该模型最早见于1964年全国高考，那是试题没有涉及临界条件，仅为机械能守恒和圆周运动的结合。2005年广东（12分），2005年北京（16分），2006年全国卷（16分），2007年全国2卷（16分），2014年全国二卷、2016年海南卷、2017年全国卷都是选择题，2018年全国卷3卷（20分）都是以这个模型直接入题。还未统计有（动能定理）摩擦阻力参与（同功能关系）解决问题以及电场或电场与重力场复合的类型模型。2007年全国2卷就是人教版教材习题没有高于教材的翻版。

如果将模型扩展，引入阻力做功，引入电场或电场与重力场复合将会演变出无穷无尽的“高考试题”，可以相信，只要有高考，这个模型就会出现，这就是永恒的经典。

二、教学目标

1.物理观念：

通过机械能守恒的例子，知道机械能守恒的条件，能解释生活中的机械能守恒的现象，形成能量守恒的观念。

2.科学思维:

①　通过感受分离和视频观察脱轨点，分析出分离的本质临界条件，应用牛顿第二定律定量计算出到达轨道最高点的运动学条件，提升科学推理和评估科学证据的能力。

②　通过分析过山车的安全问题，将生活中的情境问题转化为物理问题，提升模型建构的意识和能力。

3.科学探究：

通过小球能否到达圆形轨道的最高点的实验探究，定性研究到达圆形轨道最高点的条件，知道等高点释放并不能到达圆形轨道最高点。

4.科学态度与责任：

通过猜想与实验验证，观察到现象与猜想不符，激发兴趣和求知欲，增强探索的内驱力。

三、教学设计与讨论

1. 学生看书自主复习，回顾机械能守恒定律的内容、条件和表达式

①　内容：在只有重力或弹力做功的物体系统内，物体系统的动能和势能相互转化，但机械能的总能量保持不变。

②　条件：只有重力或弹力做功

③　表达式

2.用机械能守恒定律解释伽利略理想斜面实验（学生解释）

前面的学习中，通过伽利略理想斜面实验知道了：如果斜面光滑，小球总能到达小球释放的等高点。现在你能运用机械守恒定律解释为什么吗？

    整个过程中斜面的支持力始终和速度垂直，所以支持力不做功，只有小球的重力做功，所以机械能守恒。起电和终点速度都为0，动能相同，那么势能也应该相同，高度相等，所以小球总能到达等高点。

3.科学探究（先现象，后本质）

（1）实验探究（定性分析）

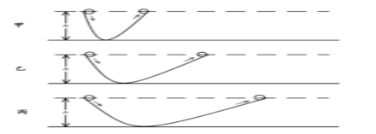
①　当h<R时，观察到小球没有到达最高点，与猜想相吻合。解释：由机械能守恒定律可知小球最高到达释放的等高点，所以不可能到达圆形轨道的顶端。（抽学生解释）

②　当h=2R时，观察到小球也没有到达圆形轨道的最高点，为什么呢？

假设小球能到达圆形轨道最高点，那么根据机械能守恒定律可知，到达圆形轨道最高点之后小球的速度为0，在圆形轨道最高点如果小球的速度为0会怎么样？（小球会竖直掉落下来，不能沿轨道做圆周运动）--并实验验证。所以，小球要想到达圆形轨道最高点速度不能为0，释放的高度一定要比2R高

③　h>2R，小球就一定能通过圆形轨道的最高点吗？

实验演示：逐渐增加h的高度。实验观察到高度不够高时，小球会脱轨掉落，要超过一定的高度小球才会到达圆形轨道的最高点。那至少要多高呢？

（2）理论探究（定量分析）

小球要想到达圆形轨道的最高点就不能脱离轨道，那如何判断小球有没有脱离轨道呢？

①　学生实验：后面同学的手用力按在前面一个同学的背上，然后悄悄地把手拿开。问：你们是怎么判断后面人的手已经拿开了？（感觉到背上没有力了）所以分离就是彼此之间没有相互作用力了，那么分离的临界条件就是刚好接触，但不挤压，也就是N刚好为0时。

②　视频观察脱轨点

③　分析圆形轨道最高点不脱离轨道的临界条件：对最高点做受力分析，小球受mg和轨道向下的弹力N，当小球刚好碰到轨道，但不挤压轨道时，N=0，只受重力。

④　那重力在这儿起到什么作用呢？小球沿轨道做圆周运动，需要向心力！这里的向心力靠重力来提供：

由牛顿第二定律得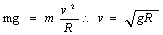： ，所以要想到达圆形轨道最高点，小球速度至少为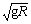

如果v小于临界值，提供的mg大于需要的向心力，小球就会做近心运动，不能到达最高点，脱轨掉下来；如果v大于临界值，提供的mg不够了，挤压轨道产生向下的弹力，由mg+N来提供向心力（带领学生分析）

小球需要多高释放才能达到这个速度呢？在07年的全国2卷中就考到了这个问题！（学生通过机械能守恒定律进行推导）-- 链接高考

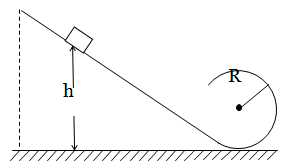
例1：（07，全国2卷）如图所示，位于竖直平面内的光滑轨道，由一段斜的直轨道和与之相切的圆形轨道连接而成，圆形轨道的半径为R。一质量为m的小物块从斜轨道上某处由静止开始下滑，然后沿圆形轨道运动。要求物块能通过圆形最高点，且在该最高点与轨道间的压力不能超过5mg（g为重力加速度）。求物块初始位置相对于圆形轨道底部的高度h的取值范围。

4.归纳解题步骤

①　判断机械能是否守恒

②　选定研究过程中的初态和末态，并确定两个状态的机械能

③　根据机械能守恒建立方程

④　解方程求出未知量

5.举一反三 -- 绳模型（等价）

如果把这儿换成绳拉小球做圆周运动一不一样呢？为什么？（实验演示）

6.灵活运用（学生讨论环节）

例2：假如你是出题人，你会怎么命题呢？（学生分享自己出的考题）

例如:小球不脱轨的条件是什么？--考试难点：多解性问题（用实验演示）

①　能上最高点：h>2.5R

②　在下半轨道来回摆动：h<R

7.情境问题（原创题）

构建物理模型：将生活中的情境转化为物理问题，解决生活实际问题。

例3：游乐场的过山车可以底朝上在圆轨道上运行，游客却不会掉下来（如图），十分刺激。现有一过山车圆轨道半径为10m，如何才能保证过上车既安全又刺激呢？（已知普通人能承受的最大加速度为6g（g取10m/s2），并且不考虑摩擦等阻力的影响。）

参考文献

吴恒德.关于“机械能守恒的条件”[N].西安邮电学院学报，2003-07.

龚劲涛，吴英.对机械能守恒定律条件的认识[N].绵阳师范学院学报，2006-10.

李庆国.机械能守恒吗？[J].物理教学探讨,2010(6):39-40.