[作者简介]朱生（1982.10-），男，汉族，吉林长春人，硕士研究生学历，吉林工商学院讲师，研究方向为应用数学及高等数学教学。

通讯地址：吉林省长春市朝阳区南湖街道卫星路7440号，远创国际。邮编：130012。电话：13943045585

一、 相关引理

二、 矩阵与对角矩阵相似时P的求法

如何求矩阵P(相似变换矩阵),使得 P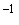AP更加简单，下面分两种情况讨论.

由定理1我们知道，如果n阶矩阵A与对角矩阵相似，那么A有n个线性无关的特征向量，此时对角矩阵可以由A的特征值得到，相似变换矩阵P就是由这n个线性无关的特征向量组成的.

根据定理2：若n阶矩阵A不与对角矩阵相似，那么它一定与Jordan标准形相似，下面将给出用初等变换求矩阵的Jordan标准形及相似变换矩阵的一种方法，先给出初等相似变换的定义：

定义3 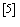 对n阶矩阵A施行下列三种变换称为初等相似变换：

（1）交换A的第i行（列）与第j行（列）之后得到B，再交换B的第j列（行）与第i列（行）

（2）用常数k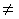0乘以方阵A的第i行（列）之后得到B，再用数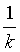乘以方阵B的第i列（行）

（3）用常数k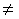0乘以方阵A的第i行（列）加到第j行（列）的相应元素上，得到矩阵B，再用数（-k）乘以方阵B的第j列（行）加到第i列（行）的相应元素上.

三、结束语

相似变换是线性代数研究的一项重要内容，它的计算方法已经渗透到了计算机科学、信息技术、人工智能等诸多工程领域，并发挥着越来越多的作用，为了适应当今科技飞速发展，培养学生逻辑思维和抽象分析解决问题的能力，有必要深入研究相似变换矩阵的求法，为此本文给出了标准形中相似变换矩阵P的两种求法，并通过实例给出计算过程，最终达到求解相似矩阵P的目的。这些结论与实例在《线性代数》教学中有一定补充与参考意义，能使学生对相似矩阵有更全面深入的了解.

参考文献

[1].屠伯损.复旦大学数学系 . 高等代数 [M].上海:上海科学技术出版社.1987.

[2]. 王耕禄. 矩阵理论 [M] .北京: 国防工业出版社. 1988.

[3]. 王萼芳. 高等代数[M].上海 : 上海科学技术出版社. 1981.

[4]. 北京大学数学系几何与代数教研室代数小组 . 高等代数[M].2002.

[5]. 张会平. 一类矩阵相似性的研究. [J]: 厦门大学学报(自然科学版)

2010.05.