一、数学数形结合思想方法

数形结合是将抽象的数与具体的形结合解决问题的思想。“数”是数学公式等，“形”是几何图形等，利用代数解释几何问题，使抽象的数学问题更加直观。数形是数学研究的重要概念，数学思想是对数学知识的本质认识，主要包括数形结合、化归分类思想等，教学中应用数学思想才能内化知识，提高数学知识应用能力。数形之间相辅相成，相互转化，数形结合思想提供解题方法是解题的指导思想，是抽象与形象思维的完美结合，实现数学问题解决方法最优化。数形结合思想是数形相互转化，构造具体形象的几何图形，利用数的准确严谨性解释图形信息。数轴的建立使人们对数形统一产生新的认识，笛卡尔将数轴拓展到平面直角坐标系，将坐标系点与有序实数对应，坐标系有对应点，代数中的方程与坐标系曲线有对应关系，笛卡尔创立解析几何学科是代数与几何结合的产物，达成数形的统一。解析几何出现后数形关系密切，产生微积分等学科。

二、数形结合思想与高中数学教学的深度融合

（一）数形结合在几何解题中的应用

例1已知空间几何体ABCD-A1B1C1D1的形状如图1所示,连接此几何体表面的某两点,得到空间直线.将该几何体沿着得到的直线旋转,旋转角度为α(0°<α<360°),得到的几何体与原几何体重合,则称此直线为该几何体的旋转轴.则正方体的旋转轴有()条.A.7B.9C.13D.14.分析根据题目所给出的几何体对称轴定义,结合题目所画的正方体示意图讨论正方体的对称轴个数.此题属于简单题,但需要注意的是情况较多,容易混淆和遗漏,是个易错题,而在解答此题目是需要注意的是分情况讨论,将所有情况考虑全面.解结合题中所给正方体ABCD-A1B1C1D1示意图2,由几何体对称轴的定义,将从以下三大类进行讨论:(1)连接正方体两个对立面的中心,得到连线如上图1EF所示,正方体围绕此直线旋转,最小旋转90°即可与自身重合.由于正方体对立面有三组,故此类情况下共有3条直线;(2)连接正方体对角的两点,得到正方体体对角线如下图3BD1所示,正方体围绕此直线旋转,最小旋转120°即可与自身重合.由于正方体体对角线共有4条,故此类情况下共有4条直线;(3)连接正方体对棱的中点,得到正方体体对棱中线如下图3MN所示,正方体围绕此直线旋转,最小旋转180°即可与自身重合.由于正方体中相对应的棱线共有6组,故此类情况下共有6条直线;综上,正方体体对称轴共有3+4+6=13条,C选项符合题意.注在处理立体几何问题过程中,由于空间立体几何对学生的空间想象思维较强,单纯依靠图形解题难度较大,为突破空间立体几何教学难关,可以将空间几何图形与代数数值相结合,使图形描述更加精准,图形中的数学条件更加清晰.

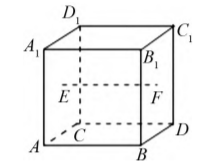
图1

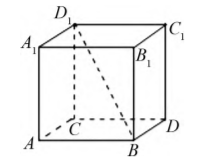
图2

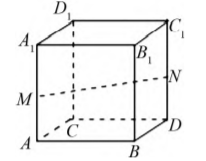
图3

（二）化形为数，提高解题效率

通过化形为数，能够有效提高解题效率，帮助学生精准把握题目的主要信息，分辨解题的主要途径，从而完善自身学科素养，在小组合作的氛围当中感受到个人的思维漏洞，意识到思考的不足之处，从而及时调整学习方向，明确概念关系。将图形中的数量抽离出来，能够有效提高解题效率。教师需要顺应高中生的认知能力和既有知识经验，选择合适的题目进行讲解，切实提高学生的解题效率。例如，在讲解高中数学三角函数图像与性质的过程中，要求学生画出函数图像，首先带领大家运用描点方法列出数据表格，通过观察图像的方法，解答函数问题，借助这样的方式化形为数，将图形转化成语言和符号等，引导学生应用数形结合思想展开小组讨论，共同参与到函数的概念分析过程中，使之明确解决三角函数问题的高效办法，利用化形为数的方法巧求方程解的数量，不断提升解题效率。

（三）塑造学生的数学抽象逻辑思维能力

高中数学教师要引导学生深入地研究数学课本，把数形结合教学模式有效地融合进去，帮助学生化解高中数学知识难点，鼓励学生自觉探索数学知识。借助数形结合的方式，学生能够深入挖掘数学逻辑思维，对数学问题进行有效分析，锻炼学生的数学能力，从而实现良好的数学课堂教学。如在教学“函数与方程”这节课时，教师可以充分借助数形结合教学模式，此节课的目标之一是需要学生知道方程的根与函数的零点（函数和两个坐标轴的交点）之间的关系，并把一元二次方程的根借助函数图象展示出来，让学生能够借助函数图像对方程的根的个数进行判断。　

结束语

综上所述，数形结合模式在高中数学教学实践中的运用是新教育发展的新要求。所以在教学过程中，数学老师要高效率地运用数形结合教学模式，为学生创设、提供优质的数学课堂，这就需要教师结合学生的实际和教学内容，有效地融合数形结合教学模式。

参考文献

[1]李强.浅谈数形结合思想在高中数学教学中的体现[J].天天爱科学(教学研究),2019(12):159.

[2]裴承雄.数形结合思想在高中数学教学中的运用研究[J].成才之路,2019(36):65-66.