一、在某些物理作用过程中，因为时间极短，学生往往是将其作用过程直接忽略，从而导致使用规律解题时出现严重错误。

 例： （新课标全国二卷）如图所示，光滑水平直轨道上有三个质量均为m的小球A、B、C。B在左侧固定一轻弹簧（弹簧左侧挡板质量不计）。设A以速度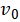朝B运动，压缩弹簧；当A、B速度相等时，B与C恰好相碰并粘接在一起，然后继续运动。假设B与C碰撞过程时间极短。求从A开始压缩弹簧直至与弹簧分离过程中：

（1）整个系统损失的机械能。

（2）弹簧被压缩到最短时的弹性势能。

解：本题运动过程较为复杂，为了帮助学生理清运动过程，我们可以设置一系列问题：

l 机械能在哪个地方损失了?

l 损失之前具有什么能量？之后又具有什么能量？

l 损失之前是什么运动状态？各物体速度怎样？

l 损失之后是什么运动状态？各物体速度怎样变化？

l 怎样求出损失之前各物体的速度与损失之后各物体的速度？

在这个问题中因为碰撞时间非常短，学生往往会将碰撞过程看成是一个状态，从而将基本物理过程分析错误。实际上本题可分为四个状态与三个过程，运动过程示意图如下：

状态1：A球以速度V₀与弹簧刚接触时。

状态2：A、 B球以共同速度V_AB将弹簧压缩最紧又刚好与C球接触而没有碰撞时。

状态3：B与C求发生碰撞后，此时B、C共速而A以速度V_AB运动。

状态4：A速度减为V_A与弹簧分离。

过程1：A、 B压缩弹簧。

过程2：B、C碰撞。

过程3：弹簧恢复，A减速，B、C加速。

实际上，每一个过程都具有初、末两个状态，过程与状态就这样联系起来了。

二、有些运动过程非常复杂，我们需要通过加速度或速度的突变来辅助分析，而加速度与速度的突变也是许多问题的临界状态，在实际问题中也很难把握，我们来看下面的例子。

 例3：固定在地面上的倾角为θ、长为2L的光滑的斜面，其下端固定一根劲度系数为K、原长为L的弹簧，弹簧与斜面平行，在斜面顶端有一质量为m的小球静止释放，如图5。       

求：弹簧压缩过程小球在那个位置速度最大？

                            图5

这个问题学生容易出现的一个错误为：小球在与弹簧接触时速度最大。想要这个问题就很容易得到简答，我们可以将弹簧被压缩过程分为三个过程和四个状态来分析，。

状态1：小球释放瞬间，速度位零，如图6。

状态2：小球运动到弹簧原长刚好与弹簧接触，如图7。

状态3：弹簧弹力大小等于重力下滑分力时，此时小球速度最大，加速度为零，如图8。

状态4：小球速度减小为零，弹簧压缩量最大，如图9。

过程1：介于第1个状态到第2个状态之间，小球作匀加速直线运动，  。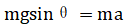

过程2：介于第2个状态到第3个状态之间，随着弹簧压缩量增大，弹力增大，小球加速度减小，直至弹力等于小球下滑分离时加速度为零，速度最大，。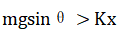

过程3：介于第3个状态与第4个状态之间，弹簧形变量越来越大，弹力大于重力下滑分力，小球做加速度增大的减速运动，直至速度减小为零，。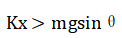

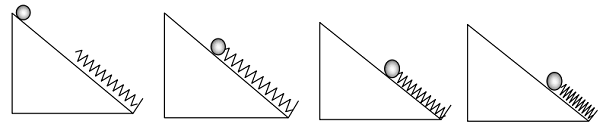
 图6（状态1）         图7 （状态2）        图8 （状态3）     图9（状态4）

     这在个问题中速度最大应该出现在状态三，因为第一个过程与第二个过程都是加速，第三个过程减速。

总结：分析清楚物理过程是解决问题至关重要的一步，恰恰是这一步难倒很多同学；同时，通过对物理过程的分析也能锻炼学生的建模能力、抽象能力、逻辑思维能力等。

想要让学生在遇到物理问题时弄清物理过程应该注意以下几点：一、有些过程作用时间虽然短，但是不能将其看作一个简单的状态，比如碰撞。二、平时分析时尽量要让学生搞清楚一些基本的临界状态，理清楚每个运动过程都有出状态和末状态，而每一个状态都是连接上一个过程和下一个过程的桥梁。